Piuttosto di calcolare la derivata terza, quarta, ecc. della funzione seno a ogni passaggio dello sviluppo di Taylor o MacLaurin è più facile e immediato calcolare la derivata prima della precedente derivata. Ad esempio, in n=2 la funzione è -sin(0). Quindi, in n=3 la derivata prima della precedente è D(-sin(0)] = - cos(0).. Gli sviluppi in serie possono tornare utili nel calcolo di forme di indecisione del tipo `0/0`, mentre non è possibile utilizzarli per forme di indecisione `oo/oo` , dal momento che non siamo in grado di sviluppare in serie una funzione nell'intorno dell'`oo`.. Per calcolare lo sviluppo di McLaurin di una funzione assegnata si procede.

Serie de Taylor para tangente a partir de las series de seno y coseno. YouTube

Sviluppo in serie di Taylor Animazione grafica YouTube

Tabella degli sviluppi in serie di Taylor (f. elementari) Altramatica
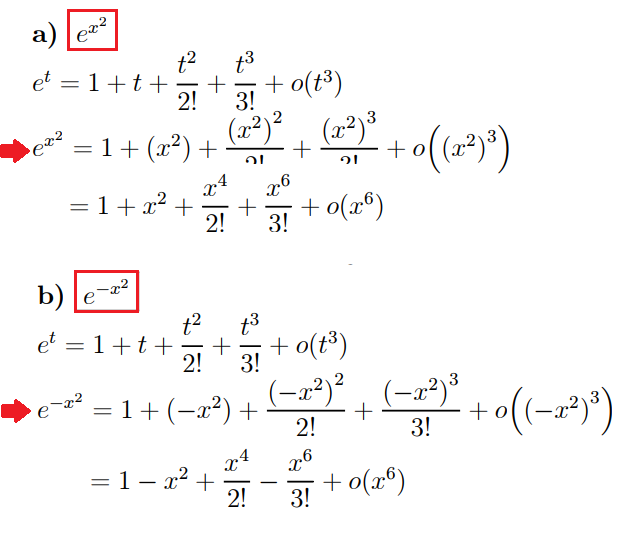
Esercizi svolti sulle Formule di Taylor e Maclaurin matematica & oltre

Visualizando aproximaciones en series de Taylor YouTube

Formula di Taylor Formula di MacLaurin Formula di Taylor resto di Lagrange .Esempi YouTube

Series de Taylor. Desarrollo en serie de la función ln(1+x) YouTube

Fasi della gravidanza calcolo e calendario settimana per settimana

Polinomios de Maclaurin y Formula de Taylor Ejercicios resueltos YouTube

Seno femminile l'anatomia e le fasi di sviluppo
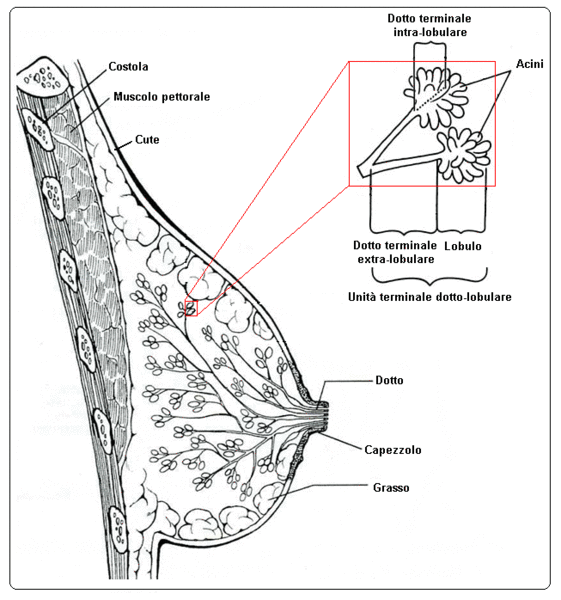
Anatomia del seno CPST (DSS) Repubblica e Cantone Ticino

Polinômios de Taylor Função seno YouTube

Serie de Taylor seno x YouTube

Polinomio de MaClaurin de la funcion seno YouTube

Serie de Potencias de Taylor para la función SENO YouTube

Explicacion Serie Taylor del seno YouTube

Analisi II Lezione 14 Formula di Taylor in più variabili YouTube

Risoluzione della forma indeterminata 0/0 mediante formula di Taylor. Gli errori da non

Esercizi svolti sulle Formule di Taylor e Maclaurin matematica & oltre

Introducció a la fórmula (o teorema) de Taylor
diretta del Teorema di Taylor-Peano per il polinomio di Taylor T2k+1(sinh) di grado 2k + 1 e centro 0 per la funzione sinh: la di erenza sinhx T2k+1(sinh)(x) e o(x2k+1) per x !0. La seconda uguaglianza e conseguenza del fatto che T2k+2(sinh) = T2k+1(sinh) (i polinomi di Taylor di sinh contengono solo le potenze di x ad esponente dispari). 4. Riassunto. Lo sviluppo di Taylor di una funzione, nell'intorno di un punto x 0 dell'asse reale, è la rappresentazione della funzione come somma di un polinomio e di un infinitesimo di ordine superiore al grado del polinomio. Esso costituisce uno strumento di analisi estremamente efficace, a livello sia qualitativo sia quantitativo.